红黑树的5条性质：
1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。
这决定了红黑树是相对平衡的二叉树，其查找，删除和插入的的时间复杂度为O(log n)

树的旋转

树的旋转，分为左旋和右旋，下面介绍下左旋(右旋的原理类似)
左旋是指以某个结点current和他的右子结点right为“支轴”，使right结点成为current子树新的根结点。即将right结点成为current结点的父结点，right结点的左子结点成为current结点的右子结点。其原理图如下：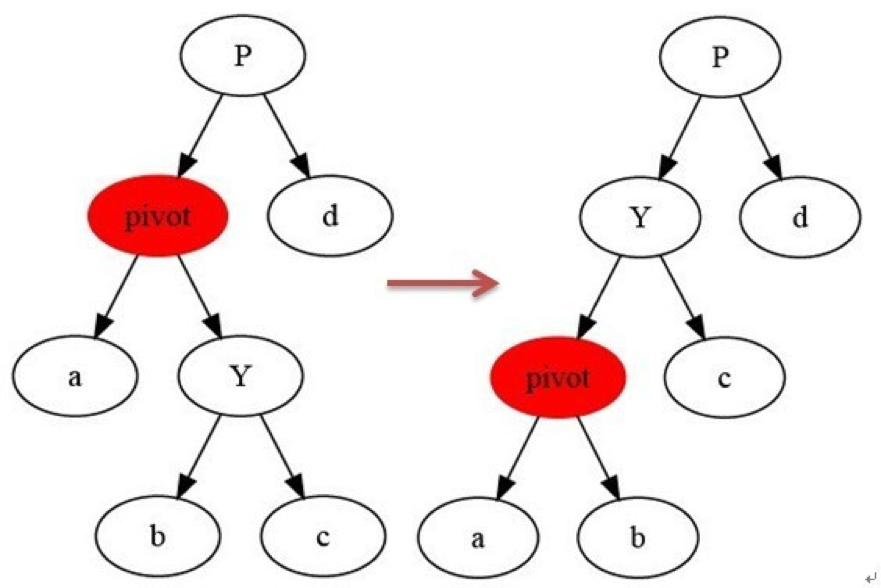

左旋操作的伪代码如下(x为上图的pivot结点)：

LEFT-ROTATE(T, x)  
y ← right[x] //Set y.  
right[x] ← left[y]      //Turn y's left subtree into x's right subtree.  
p[left[y]] ← x  
p[y] ← p[x]             //Link x's parent to y.  
if p[x] = nil[T]        //Set P's child node
   then root[T] ← y  
   else if x = left[p[x]]  
           then left[p[x]] ← y  
           else right[p[x]] ← y  
 left[y] ← x             //Put x on y's left.  
 p[x] ← y

红黑树的插入

1、 先按照二叉查找树插入的方式插入节点，然后把插入节点的左右孩子都置为叶结点nil，将插入节点涂色成红色。

2、在插入节点后，对节点进行旋转并重新着色，使整棵树保持红黑树的性质

这时会有下面几种情况：

• 如果插入的是根结点，因为原树是空树，此情况只会违反性质2，所以直接把此结点涂为黑色。
• 如果插入的结点的父结点是黑色，由于此不会违反性质2和性质4，红黑树没有被破坏，所以此时也是什么也不做。

但遇到下述三种情况时：

• 插入修复情况1：如果当前结点的父结点是红色且祖父结点的另一个子结点（叔叔结点）是红色
• 插入修复情况2：当前结点的父结点是红色,叔叔结点是黑色，当前结点是其父结点的右子
• 插入修复情况3：当前结点的父结点是红色,叔叔结点是黑色，当前结点是其父结点的左子

对于插入修复情况1，对策：将当前结点的父结点和叔叔结点涂黑，祖父结点涂红，把当前结点指向祖父结点，从新的当前结点重新开始算法
对于插入修复情况2，对策：当前结点的父结点做为新的当前结点，以新当前结点为支点左旋，把当前结点指向祖父结点，从新的当前结点重新开始算法 ，。
对于插入修复情况3，对策：父结点变为黑色，祖父结点变为红色，在祖父结点为支点右旋

可以将上面5种情况看成状态机的5种状态，包括红黑树（已经调整到位，终止状态）共6种状态。红黑树的插入就是状态机几种状态的转移。

红黑树的删除

先按照二叉查找树删除结点的方式删除结点，然后再对整棵树进行调整，使其保持红黑树的性质
也是分为几种情况分别处理（其中可能发生情况的转化），略