Fibonacci Number

Table of Contents

• Problem Formulation
• Recursive Fibonacci Parallelism

We study the classic problem, Fibonacci Number, to demonstrate the use of recursive task parallelism.

Problem Formulation

In mathematics, the Fibonacci numbers, commonly denoted F(n), form a sequence such that each number is the sum of the two preceding ones, starting from 0 and 1.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

A common solution for computing fibonacci numbers is recursion.

int fib(int n) {
  if(n < 2) return n;
  return fib(n-1) + fib(n-2);
}

Recursive Fibonacci Parallelism

We use tf::Subflow to recursively compute fibonacci numbers in parallel.

#include <taskflow/taskflow.hpp>
 
int spawn(int n, tf::Subflow& sbf) {
  if (n < 2) return n;
  int res1, res2;
  sbf.emplace([&res1, n] (tf::Subflow& sbf) { res1 = spawn(n - 1, sbf); } )
     .name(std::to_string(n-1));  
  sbf.emplace([&res2, n] (tf::Subflow& sbf) { res2 = spawn(n - 2, sbf); } )
     .name(std::to_string(n-2));
  sbf.join();
  return res1 + res2;
}
 
int main(int argc, char* argv[]) {
  
  int N = 5;
  int res;
 
  tf::Executor executor;
  tf::Taskflow taskflow("fibonacci");
 
  taskflow.emplace([&res, N] (tf::Subflow& sbf) { res = spawn(N, sbf); })
          .name(std::to_string(N));
 
  executor.run(taskflow).wait();
 
  taskflow.dump(std::cout);
 
  std::cout << "Fib[" << N << "]: " << res << std::endl;
 
  return 0;
}

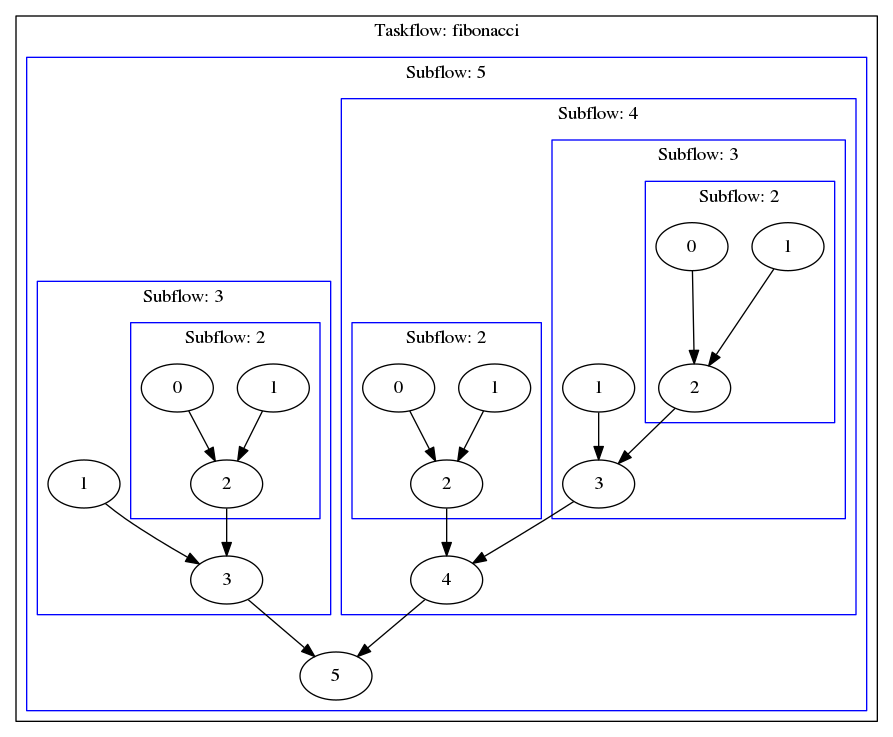
The spawned taskflow graph for computing up to the fifth fibonacci number is shown below:

Even if recursive dynamic tasking or subflows are possible, the recursion depth may not be too deep or it can cause stack overflow.